Health Event Counts and Crude, Age-specific, and Age-adjusted Rates

Table of Contents

A. Counts
B. Crude Rates
C. Age- and Sex-specific Rates
D. Age-adjusted Rates
....D.1. Age-adjusted Rates, Direct Method
....D.2. Indirectly Age-adjusted Rates, Indirect Method
E. Deciding Which Measure to Use
References

---

A. Counts

When communicating with health planning groups or legislators, the total number of health events, or the count, can convey the magnitude of the problem, the prevention effort required, or the health care that may be needed. Table 1 shows some examples of counts.

Table 1: Number of Deaths for Four Leading Causes by Cause and Sex, Utah, 2005

Underlying Cause of Death	Men	Women	Total
Disease of heart (ICD10: I00-I09, I11, I13, I20-I51)	1,408	1,437	2,845
Malignant neoplasms (ICD10: C00-C97)	1,344	1,168	2,512
Injury, Unintentional injuries (ICD10: V01-X59, Y85-Y86)	466	249	715
Respiratory, chronic lower respiratory diseases (ICD10: J40-J47)	335	257	592

---

B. Crude Rates

The count alone will be less useful if you want to compare populations of unequal size. Knowing the population sizes is useful, but computing a rate will allow direct comparison between similar populations. A rate is a fraction that typically has four components:

In general, a rate is called a "crude rate" if it has not been adjusted for the age and sex composition of a population.

Table 2 shows an example of crude rate calculations for heart disease by local health districts. The example, which is a three year time period, averages the number of deaths occurring per year divided by the population to produce the crude death rates for the period.

Table 2: Crude Death Rate for Heart Disease by Local Health District, Utah, 2003-2005

Utah Local Health District	Average Annual Number of Deaths	Average Annual Population Estimate	Crude Death Rate (Deaths per 100,000 Population)
Bear River LHD	168	147,371	113.77
Central Utah LHD	149	70,382	211.7
Davis County LHD	278	269,744	102.94
Salt Lake Valley LHD	1,081	957,972	112.84
Southeastern LHD	83	52,936	156.79
Southwest LHD	286	174,363	164.03
Summit County LHD	22	35,149	61.64
Tooele County LHD	56	50,388	111.14
TriCounty LHD	68	42,277	161.63
Utah County LHD	404	438,995	92.03
Wasatch County LHD	17	19,230	90.14
Weber-Morgan LHD	312	217,939	143.16

Using the values, above, for Bear River LHD as an example...
The calculation for the Bear River LHD heart disease crude death rate for 2003-2005 looks like this:

---

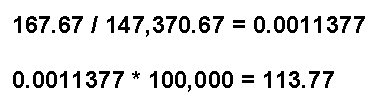
FAQs for Crude Rates:

Combining Years

Q: I am looking at death rates for a five-year period. What should I use for a population denominator?
A: If you are combining numerator values over the five years by summing them, then use the sum of the population counts over the same period. If you are combining numerator values by taking an average, then take an average of the population counts for the same time period and geographic area. Alternatively, you could also use an average over the five years in the numerator, and a "mid-point" population estimate, that is, a population estimate for the mid-point, or middle, year in the denominator.

Back to Top

---

C. Age- and Sex-specific Rates

An age-specific rate is calculated by dividing the total number of health events for the specific age-group of interest by the total population in that age group. In Table 3, the age- and sex-specific rates for suicide are shown. The example demonstrates that the greatest number of suicides occur among adolescents and young adults, whereas the highest rate occurs among elderly men.

The calculation for an age-specific rate is the same as for a crude rate.

Table 3: Suicide Mortality Rates by Age and Sex, Utah, 2002-2006

	Males	Females

Age Group	Suicide Deaths	Population	Age- and Sex-specific Rate per 100,000 Population	Suicide Deaths	Population	Age- and Sex-specific Rate per 100,000 Population
<15	13	1,677,087	0.78	5	1,587,965	0.31
15-44	852	2,921,606	29.16	199	2,838,704	7.01
45-64	372	1,153,370	32.25	117	1,163,236	10.06
65+	168	474,715	35.39	23	587,013	3.92

Back to Top

---

D. Age-adjusted Rates

Crude rates are valuable for comparing similar population of different sizes, but the word, "similar" is a key concept, because crude rates can be misleading when comparing rates for populations with different age compositions. The crude mortality rate for a population depends on the mortality rate in each age group as well as on the proportion of people in each age group. For instance, the crude rate for most causes of death will be higher in populations with a large proportion of elderly individuals, and lower in populations with a large proportion of young individuals. An age-adjusted rate may be used to compare mortality or disease risk in two populations with with different age compositions.

An adjusted rate is an overall summary measure that helps control for age differences between populations. When comparing across geographic areas, some method of age-adjusting is typically used to control for area-to-area differences in health events that can be explained by different age distributions in the area populations. For example, an area that has an older population will have higher crude death rates for cancer, even though its exposure levels and cancer rates within specific age groups may be the same as those in other areas. One might incorrectly attribute the high cancer rates to some characteristic of the area other than age. Age-adjusted rates control for age effects, allowing better comparability of rates across areas. Age-adjustment may also be used to control for age effects when comparing across several years of data, as the age distribution of the population changes over time.

Calculating age-adjusted rates using "direct age standardization" is the same as calculating a weighted average. It adjusts the age-specific rates observed in a given population (such as a county or ethnic group) to the age distribution of a standard population (Lilienfeld & Stolley, 1994). In some cases, such as when there are too few cases to stratify by age, "indirect age standardization" may be used. Indirect standardization is based on standard mortality and morbidity ratios (SMR), and adjusts the age-specific rates found in the standard population to the age distribution of the smaller area or sub-population.

In 1998, the Centers for Disease Control and Prevention (CDC) revised the standard population weights for age-adjustment (Klein & Schoenborn), replacing the 1940 U.S. standard population weights that had been used for the previous several decades. Table 4, below, contains the standard population weights published by the CDC. They represent the proportion of the U.S. 2000 population in each age group, and sum to 1.0.

Table 4. U.S. 2000 Standard Population Weights for Age Standardization

	Age Group	U.S. 2000 Population Projection (in thousands)	Weight
1	Under 1 Year	3,795	0.013818
2	1 - 4 Years	15,192	0.055317
3	5 - 14 Years	39,977	0.145565
4	15 - 24 Years	38,077	0.138646
5	25 - 34 Years	37,233	0.135573
6	35 - 44 Years	44,659	0.162613
7	45 - 54 Years	37,030	0.134834
8	55 - 64 Years	23,961	0.087247
9	65 - 74 Years	18,136	0.066037
10	75 - 84 Years	12,315	0.044842
11	85 Years and Over	4,259	0.015508

Back to Top

---

D.1. Age-adjusted Rates: Direct Method

To apply direct age-adjustment to a set of rates, the age-specific rate for each age group in the study population is multiplied by the appropriate weight in the standard population. The sum of these products is the directly age-adjusted, or age-standardized rate. The age-adjusted rate can be considered an average of each of the individual age-specific rates, but rather than being a simple average, it is a weighted average with each age-specific rate weighted by the proportion of people in the same age group in the standard population.

Tables 5a and 5b demonstrate the method used by IBIS-Q in calculating age-adjusted rates. Notice that using crude death rates in Tables 5a and 5b, one might conclude that persons in Southwest LHD have a higher underlying risk for unintentional injury death compared with the state of Utah. How should the age-adjusted death rates be interpreted? You could use confidence intervals to assist in interpreting these data (IBIS automatically provides 95% confidence intervals for all rates).

Table 5a. Age-adjusted Death Rate for Unintentional Injuries, State of Utah, 2002-2006

Age Group	Number of Deaths (5-Year Sum)	Population Counts (5-Year Sum) (1)	Age- specific Rate (2)	U.S. 2000 Std Pop Weight	Cross Products (3)
Under 1 Year	42	250,611	16.76	0.013818	0.231576
1 - 4 Years	121	960,731	12.59	0.055317	0.696694
5 - 14 Years	130	2,053,710	6.33	0.145565	0.921428
15 - 24 Years	560	2,253,594	24.85	0.138646	3.445242
25 - 34 Years	452	1,957,687	23.09	0.135573	3.130173
35 - 44 Years	369	1,549,029	23.82	0.162613	3.873665
45 - 54 Years	394	1,405,684	28.03	0.134834	3.779270
55 - 64 Years	297	910,922	32.60	0.087247	2.844630
65 - 74 Years	256	564,672	45.34	0.066037	2.993857
75 - 84 Years	396	372,361	106.35	0.044842	4.768875
85 Years and Over	443	124,695	355.27	0.015508	5.509478
All Ages	3,462	12,403,696	27.91 (4)	1	32.19 (5)

Table 5b. Age-adjusted Rate for Unintentional Injuries, Southwest LHD, Utah, 2002-2006

Age Group	Number of Deaths (5-Year Sum)	Population Counts (5-Year Sum) (1)	Age- specific Rate (2)	U.S. 2000 Std Pop Weight	Cross Products (3)
Under 1 Year	5	16,753	29.85	0.013818	0.412404
1 - 4 Years	13	62,149	20.92	0.055317	1.157092
5 - 14 Years	18	135,238	13.31	0.145565	1.937451
15 - 24 Years	51	157,563	32.37	0.138646	4.487694
25 - 34 Years	34	117,343	28.97	0.135573	3.928212
35 - 44 Years	32	94,544	33.85	0.162613	5.503909
45 - 54 Years	23	91,791	25.06	0.134834	3.378525
55 - 64 Years	34	72,058	47.18	0.087247	4.116681
65 - 74 Years	25	64,701	38.64	0.066037	2.551622
75 - 84 Years	28	48,070	58.25	0.044842	2.611974
85 Years and Over	39	15,410	253.08	0.015508	3.924802
All Ages	302	875,620	34.49 (4)	1	34.01 (5)

(1) The Utah Population Estimates Committee (UPEC) and the Governor's Office of Planning and Budget (GOPB), Estimates for Counties by Sex and Single Year of Age.

(2) Rate per 100,000 = (Age-specific death count * 100,000) / Age-specific population count

(3) Age-specific death rate * U.S. 2000 Std Pop Weight

(4) Crude death rate

(5) Age-adjusted rate

According to Curtin & Klein, "One of the problems with [direct age adjustment] is that rates based on small numbers of deaths will exhibit a large amount of random variation. A very rough guideline is that there should be at least 25 total deaths over all age groups." When fewer than 25 health events occurred over a time period, you may consider combining years, or using indirect age-adjustment.

Age adjustment is not appropriate if the age-specific death rates in the population of interest do not have a consistent relationship. For example, if death rates among younger persons is increasing, but death rates among older persons is decreasing. One's conclusion of the trend in this death rate would be different, depending on which standard population is used. A younger standard population (such as the U.S. 1940) would show an increase, whereas an older standard population (such as the U.S. 2000) would show a decrease, or no change at all. One's selection of the standard population should not affect the comparisons. For more information, see Curtin & Klein.

When reporting age-adjusted rates, always report the standard population used, and when comparing results to other data, be sure to document that those data were also age-adjusted and report the standard population. The age-adjusted rate is hypothetical, and is useful only for comparing populations, either over time, by geographic area, by sex, or by racial/ethnic subgroups.

Back to Top

---

FAQs for Age-adjustment:

Event Rates for a Subpopulation

Q: I am looking at death rates for female breast cancer. Which standard population should I use, females in U.S. 2000 or all persons?
A: Theoretically, it doesn't matter, as long as you use the same standard population for all your analyses. But the recommended standard population is now the U.S. 2000 total population, even for analyses that apply only to a particular sex, race, or other subgroup.

When NOT to Age-adjust

Q: Are there times I should NOT age-adjust?
A: Yes. Do NOT use age-adjustment when...

Age Subpopulations

Q: I am looking at adults, only. If I use the weights in Table 4, above, they will not sum to one. Is that okay?
A: No. The weights must always sum to one. Weights for certain age subgroups have been published by the CDC. But you may also recompute the proportions in Table 4, using only the age range that is relevant to your analysis.

Age/Sex Adjusted Rates

Q: I have a report that uses age AND SEX adjusted rates. What is this, and why doesn't IBIS produce age and sex adjusted rates?
A: It is sometimes appropriate to adjust by other variables besides age. Rates that have been adjusted by age and sex use age- and sex-specific rates, weighted by twice the number of weights (one set for males and one set for females), but the total of all the weights still must sum to 1.0. IBIS-Q doesn't compute these rates because there is little demand for it.

Confidence Intervals for Age-adjusted Rates

Q: Can I use the confidence interval for the crude rate with the age-adjusted rate?
A: No, a new confidence interval for the age-adjusted rate must be calculated. Methods for calculation of this confidence interval may be found in Curtin & Klein.

Back to Top

---

D.2. Age-adjusted Rates: Indirect Method

The direct method can present problems when population sizes are particularly small. Calculating directly standardized rates requires calculating age-group-specific rates, and for Utah Small Areas these age-specific rates may be based on one or two events. In such cases, indirect standardization of rates may be used.

Indirectly standardized rates are based on the standard mortality or morbidity ratio (SMR) and the crude rate for a standard population. Indirect standardization adjusts the overall standard population death rate to the age distribution of the small area (Lilienfeld & Stolley, 1994). It is technically appropriate to compare indirectly standardized rates only with the rate in the standard population, not with each other.

---

E. Deciding Which Measure to Use

So, how do I know which one to use!? You will want to use the measure that best informs the question you are trying to answer. This is a guideline, not a hard and fast rule, but generally:

If your question is:	Then use:
MAGNITUDE: How big is the problem?	Number of events (count)
PROBABILITY: What is the underlying risk in my population?	Crude rate and confidence interval
DISPARITY: Is there a difference in risk after controlling for age?	Age-adjusted rate and confidence interval

Back to Top

---

1. Anderson RN, Rosenberg HM. Age Standardization of Death Rates: Implementation of the Year 2000 Standard. National vital statistics reports; vol 47 no.3. Hyattsville, Maryland: National Center for Health Statistics. 1998.

2. Klein RJ, Schoenborn CA. Age-Adjustment Using the 2000 Projected U.S. Population. Statistical notes; no.20. Hyattsville, Maryland: National Center for Health Statistics. January 2001.

3. Curtin, LR, Klein, RJ. Direct Standardization (Age-Adjusted Death Rates). Statistical notes; no.6. Hyattsville, Maryland: National Center for Health Statistics. March 1995.

4. Fleis, JL. Statistical methods for rates and proportions. John Wiley and Sons, New York, 1973. As cited in Curtin and Klein, 1995.

5. Klein RJ, Schoenborn CA., 2001.

6. Lilienfeld, DE and Stolley, PD. Foundations of Epidemiology, 3rd Ed. Oxford University Press, 1994.